 Zerodha (Trading & Demat Account)
Zerodha (Trading & Demat Account)
FREE Equity Delivery and MF
Flat ₹20/trade Intra-day/F&O
 Zerodha (Trading & Demat Account)
Zerodha (Trading & Demat Account)
FREE Equity Delivery and MF
Flat ₹20/trade Intra-day/F&O

|
|
Compare Short Put and Short Condor (Short Call Condor) options trading strategies. Find similarities and differences between Short Put and Short Condor (Short Call Condor) strategies. Find the best options trading strategy for your trading needs.
| Short Put | Short Condor (Short Call Condor) | |
|---|---|---|
 |
 |
|
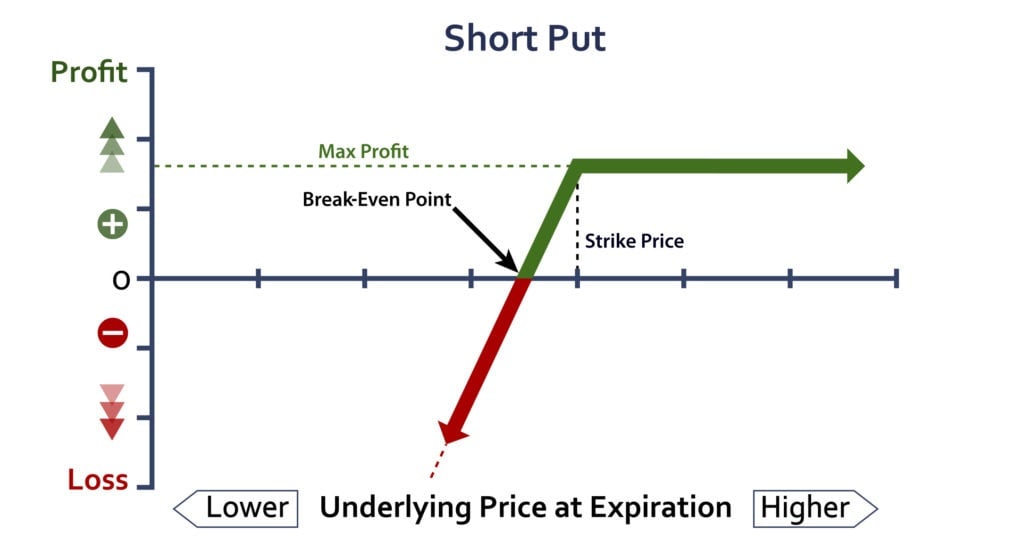
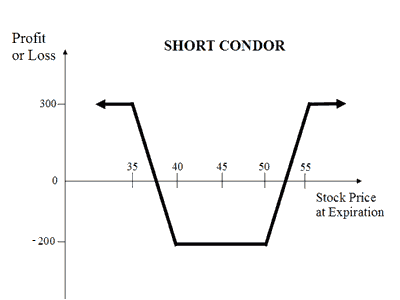
| About Strategy | A short put is another Bullish trading strategy wherein your view is that the price of an underlying will not move below a certain level. The strategy involves entering into a single position of selling a Put Option. It has low profit potential and is exposed to unlimited risk. A short put strategy involves selling a Put Option only. For example if you see that the shares of a Company A will not move below Rs 1000 then you sell the Put Option of that stock at Rs 1000 and receive the premium amount. The premium received will be the maximum profit you can earn from this trade. However, if the price of the underlying moves below 1000 then you will incur unlimited losses. | A Short Call Condor (or Short Condor) is a neutral strategy with a limited risk and a limited profit. The short condor strategy is suitable for a high volatile underlying. The goal of this strategy is to profit from a stock price moving up or down beyond the highest or lowest strike prices of the position. The strategy is similar to Short Call Butterfly strategy with the difference being in the strike prices selected. Suppose Nifty is currently trading at 10,400. If the trader is expecting high volatility in the index due to specific events i.e. budget, results, and elections, he could choose the Short Condor strategy to profit in such a market scenario. The strategy could be constructed as below: Short Condor Options Strategy ... Read More |
| Market View | Bullish | Volatile |
| Strategy Level | Beginners | Advance |
| Options Type | Put | Call |
| Number of Positions | 1 | 4 |
| Risk Profile | Unlimited | Limited |
| Reward Profile | Limited | Limited |
| Breakeven Point | Strike Price - Premium | |
| Short Put | Short Condor (Short Call Condor) | |
|---|---|---|
| When to use? | Short Put works well when you're Bullish that the price of the underlying will not fall beyond a certain level. |
The Short Call Condor works well when you expect the price of the underlying to be very volatile. In other words, when the trader is anticipating massive price movements (in any direction) in the underlying during the lifetime of the options. |
| Market View | Bullish When you are expecting the price or volatility of the underlying to increase marginally. |
Volatile When you are unsure about the direction in the movement in the price of the underlying but are expecting high volatility in it in the near future. |
| Action |
A short put strategy involves selling a Put Option only. So if you see that the shares of a Company A will not move below a 1000 then you sell the Put Option of that stock at 1000 and receive the premium amount. The premium received will be the maximum profit you can earn from this deal. However, if the price of the underlying moves below 1000 than you will incur losses. |
Buy ITM Call Option + Buy OTM Call Option + Sell Deep OTM Call Option + Sell Deep ITM Call Option Suppose Nifty is trading at 10,400. If you expect high volatility in the Nifty in the coming days then you can execute Short Call Condor by selling 1 ITM Nifty Call at 10,200, buying 1 ITM Call at 10,300, buying 1 OTM Call Option at 10, 500 and selling 1 OTM Nifty Call at 10, 600. Your maximum loss will be if Nifty closes in the range of 10,300 to 10,500 on expiry while maximum profit will be on either side of upper or lower strikes. |
| Breakeven Point | Strike Price - Premium |
There are 2 break even points in this strategy. The upper break even is hit when the underlying price is equal to the difference between strike price of highest strike shot call and net premium paid. The lower break even is hit when the underlying price is equal to the strike price of lowest strike short call and net premium paid. Lower Breakeven = Lower Strike Price + Net Premium Upper breakeven = Higher Strike Price - Net Premium |
| Short Put | Short Condor (Short Call Condor) | |
|---|---|---|
| Risks | Unlimited There is no limit to losses incurred in the trade. The risk is when the price of the underlying falls, and the Put is exercised. You are then obliged to buy the underlying at the strike price. |
Limited This is a limited risk strategy. The maximum risk in a short call condor strategy is calculated as below: Max Loss = Strike Price of Lower Strike Long Call - Strike Price of Lower Strike Short Call - Net Premium Received + Commissions Paid The max risk is when the price of the underlying remains in between strike price of 2 long calls. |
| Rewards | Limited The profit is limited to premium received in your account when you sell the Put Option. |
Limited The maximum profit in a short call condor strategy is realized when the price of the underlying is trading outside the range at time of expiration.<.p> Max Profit = Strike Price of Lower Strike Short Call - Strike Price of Lower Strike Long Call - Net Premium Paid |
| Maximum Profit Scenario | Underlying doesn't go down and options remain exercised. |
All options exercised or not exercised |
| Maximum Loss Scenario | Underlying goes down and options remain exercised. |
Both ITM Calls exercised |
| Short Put | Short Condor (Short Call Condor) | |
|---|---|---|
| Advantages | It allows you benefit from time decay. And earn income in a rising or range bound market scenario. |
It allows you to profit from highly volatile underlying assets moving in any direction. The maximum profit for the condor trade may be low in relation to other trading strategies but it has a comparatively wider profit zone. Earn profit with little or no investment as you will have a credit of net premiums. |
| Disadvantage | It is a high risk strategy and may cause huge losses if the price of the underlying falls steeply. |
Strike prices selected may have an impact on the potential of profit. Brokerage and taxes make a significant impact on the profits from this strategy. The cost of trading increases with the number of legs. This strategy has 4 legs and thus the brokerage cost is higher. |
| Simillar Strategies | Bull Put Spread, Covered Call, Short Straddle |
Long Put Butterfly, Short Call Condor, Short Strangle |

Add a public comment...

FREE Intraday Trading (Eq, F&O)
Flat ₹20 Per Trade in F&O
|
|